At Mirdin we help students to practice writing software. You might be familiar with how practicing guitar or some sport is very different from just playing/performing.

You will get better from just playing but it takes much longer and your understanding of what you have learned is much worse. You will learn what to do but have a harder time explaining what you have learned.

This is exactly how it normally is to work towards becoming a senior engineer. Senior engineers that have been through a lot gain intuition. They know that one design decision should be taken over another but they might have a hard time explaining exactly why. So do you really have to spend 10 000 hours just working on projects to achieve mastery ?

At Mirdin we believe there is a more effective way. We try to give meaning behind every design decision to not have to use gut feeling or past experiences with similar design decisions to have an opinion on what direction to take.

One way we do this is by giving students a series of short design exercises that takes just a few hours to finish but will contain a lot of opportunities for things to go wrong. Then we give the students immediate feedback on how their earlier design choices affected later requirements. With smaller groups or private students, we design specific requirements for each implementation that are meant to poke holes at a student’s design.

The Tic-Tac-Toe challenge is not exactly in this vain but instead gives students the challenge to write a Tic-Tac-Toe program that cannot go wrong, and produce compile time errors for as many incorrect uses as possible. For example, making a move with the same player twice.

When I was a student at Mirdin a few years ago I decided to try to write Tic-Tac-Toe completely on the typelevel in TypeScript. This proved to be very challenging but fun. I have now expanded on that initial attempt and written this post to explain how it works in the hope to teach some more advanced typelevel TypeScript. And maybe also make you interested in doing something similar for fun.

I have a lot to thank the excellent Type-Challenges for helping me learn enough type-level trickery to get this done. https://github.com/type-challenges/type-challenges

The post

This is going to be a post about advanced type-level programming. I’ll be showing you a sequence of functions, from top to bottom (mostly). I recommend treating each snippet like a puzzle. Try to understand how each of them works as you go along until you feel you could have written it yourself. We’ll start off small, with some academic-seeming type tweaks, but pretty soon you’ll find implementing type-level board logic a piece of cake.

I showed it to Jimmy and he was dismissive . He’s a PL Ph. D. with 10 years in Haskell, and finds type-level programming easy and uninteresting. After finishing the whole post he had a funny reaction, and shared the draft with his friends.

I hope you can have a similar experience but maybe get past the ‘I Hate it’ quicker!

It was also his idea to add the ___DISPLAY___ that i will show you in just a sec, thanks for that Jimmy!

Let’s go!

Where to find the code?

The latest code can be found here just paste it into typescript-playground to follow along.
TypeScript Playground as of 2022-09-16

First: End result demo!

There is gonna be a lot of code so to peak your interest let me present you with the end result. A UI for playing Tic-Tac-Toe on the typelevel where type errors are used to display the state of the game and provide feedback for correct play.

// ##################################
// ##################################
// #          Play a Game           #
// #              of                #
// #--------------------------------#
// #           Typelevel            #
// #          Tic-Tac-Toe           #
// #--------------------------------#
// #              UI                #
// #          STARTS HERE           #
// ##################################
// ##################################
//
// This is my attempt of a decent UX (hehe).
// 0. Select game board size (3 => 3x3, 4 => 4x4, etc)
// 1. Cross will be the first to move
// 2. Just enter coordinates as a number xy
//    (13 => Coordinate(x=1, y=3))
//
// The status checks below will turn RED
// To show what state the game is in.
//
// Illegal moves will be compile-time errors
// with decent error messages.
//
// Hover ___DISPLAY__ for a visual representation
// of the current state of the game.

Display

Current state highlighting

Error handling

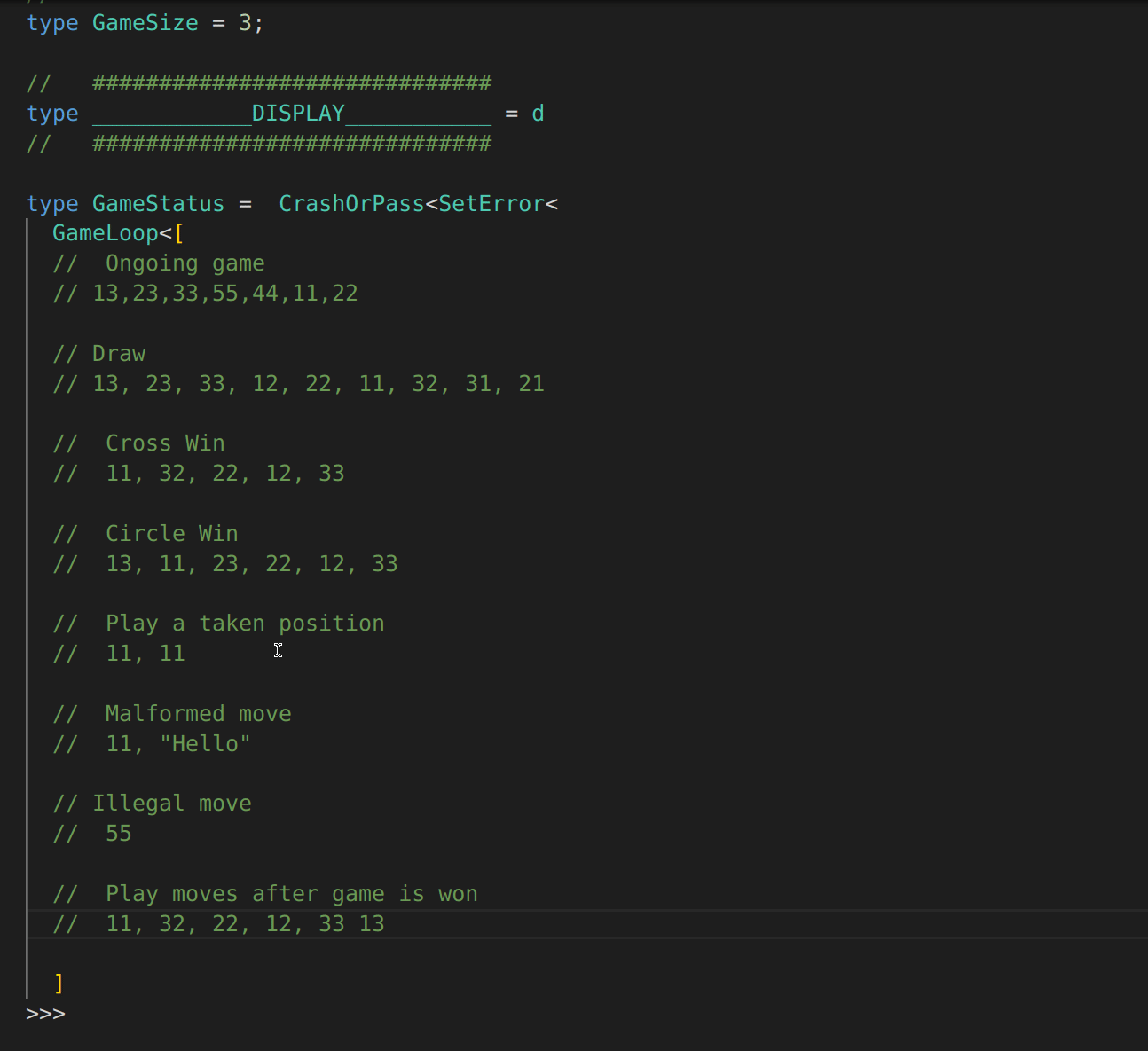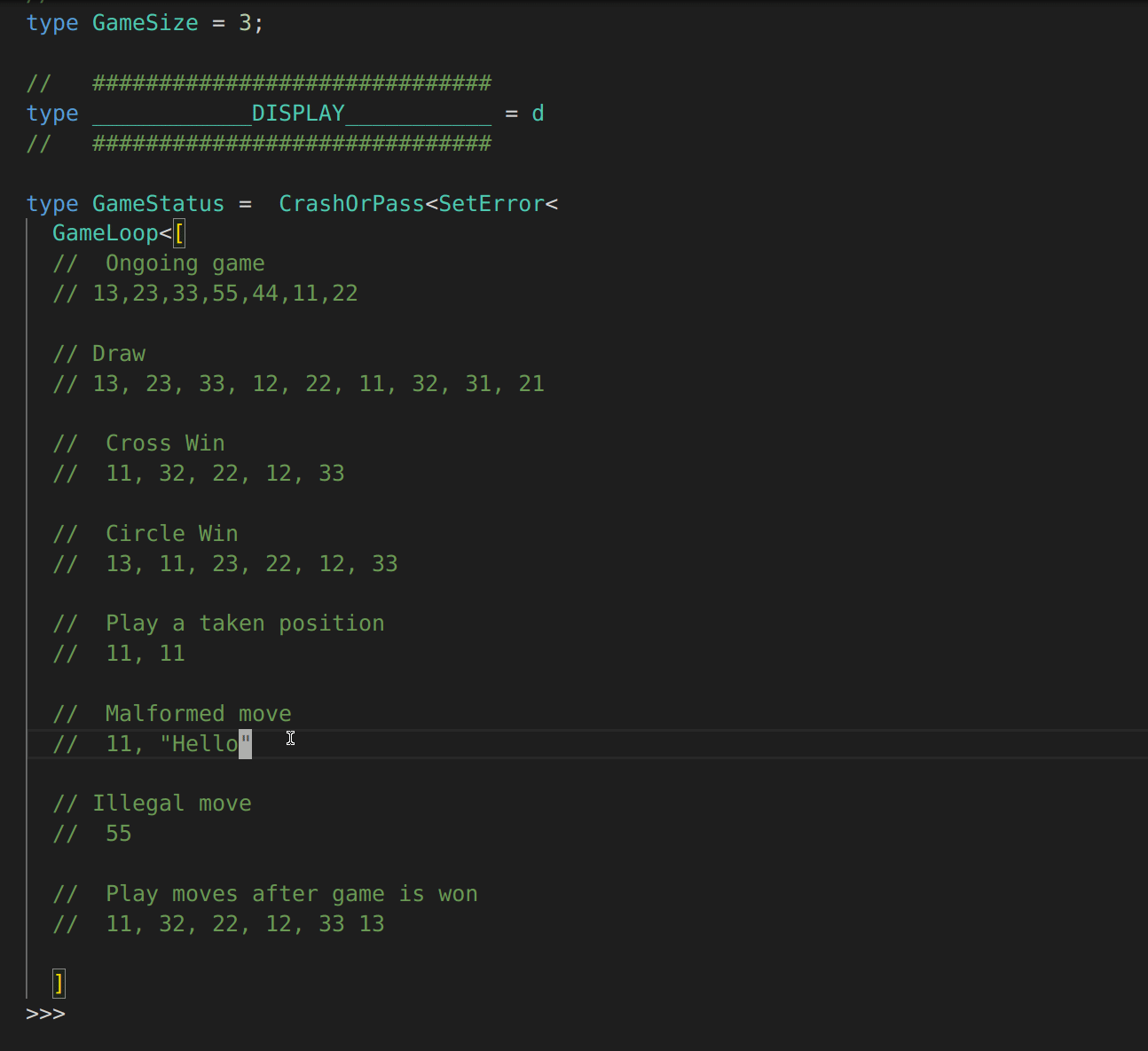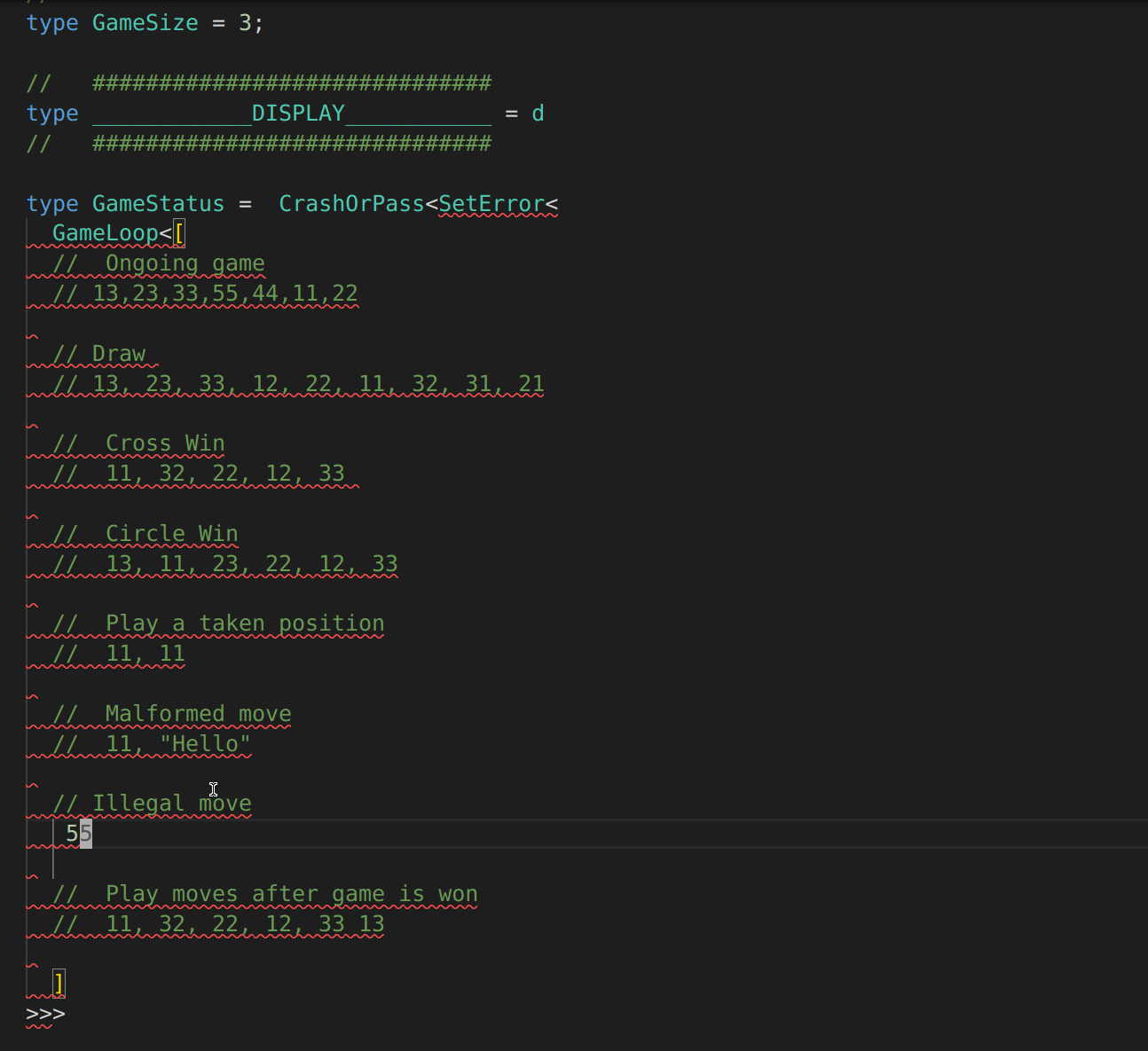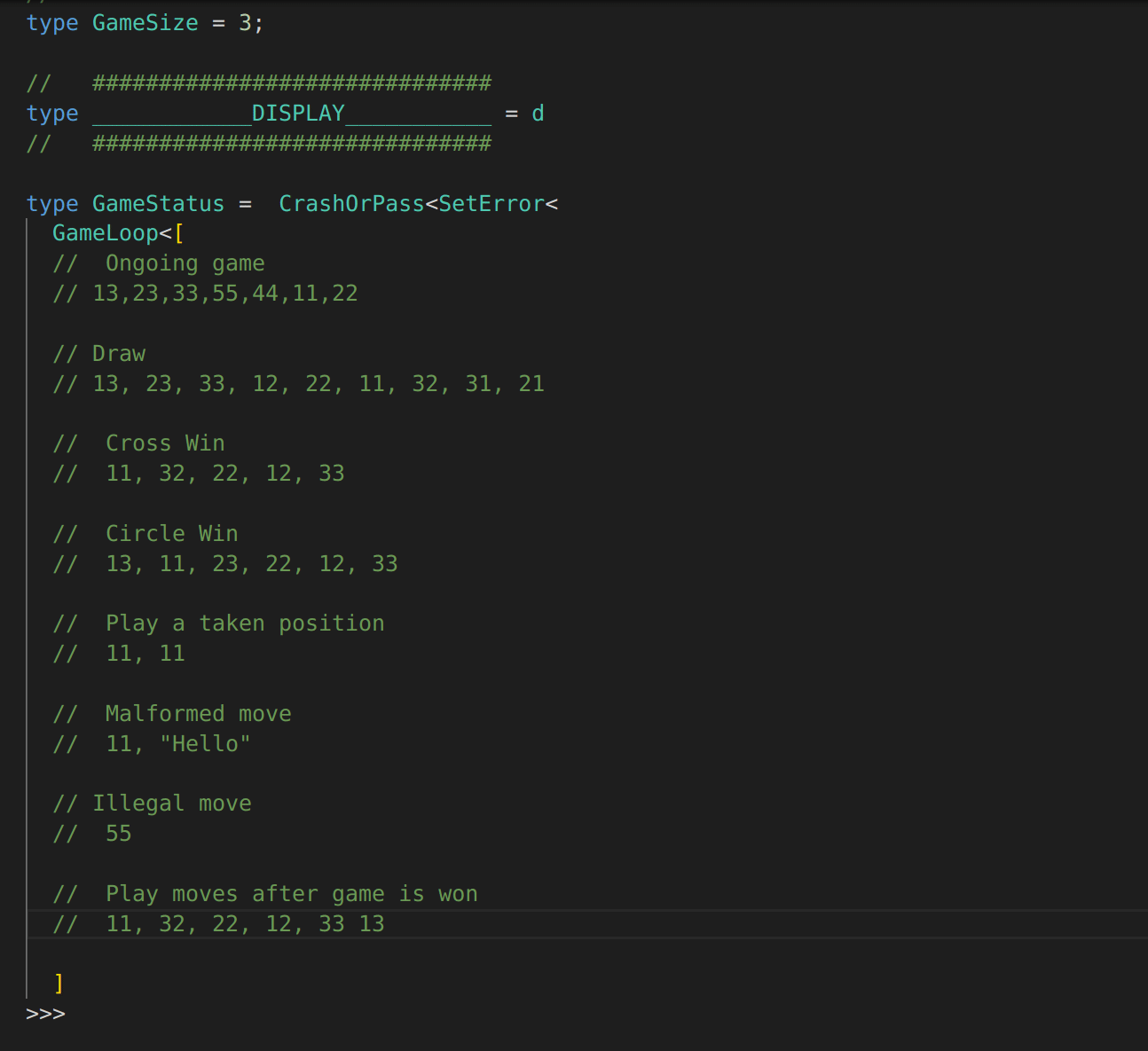
Requirements

If you would like to give this a try yourself, here are the requirements.

Design an API for a Tic-Tac-Toe board, consisting of types representing states of the board, along with functions move, takeMoveBack, whoWonOrDraw, and isPositionOccupied.

• All functions must be pure
• All functions must return a sensible value and may not throw exceptions
• A move can only be made if
  • the game is not over
  • the player is the current player
  • the move is valid (i.e. not already played)
• Calling TakeMoveBack on a board with no moves is a compile-time error
• Calling WhoWonOrDraw on a tic-tac-toe board but the game has not finished is a compile-time error
• IsPositionOccupied works for in-play and completed games.

Some extra design decisions

I wanted the game to be possible to play on boards of any size, (3x3, 4x4, 5x5, etc). To achieve this the winning positions need to be calculated from Size instead of hard-coded. This is possible but a bit fiddly. I have not yet achieved the ability to have two games of different Size in the same project. To do that I would have to parameterize the program a bit more, this is something to try in a later version (famous last words).

Show me the code!

Soon!… The reason this is written in TypeScript is that it’s the language I know best, and also the language I want to get better at the most but also TypeScript has a bunch of typelevel features that very few other mainstream typed languages have.

We will go through the code top to bottom, except for the “UI” code, which will be left for last. There are a lot of comments in the code that are also meant to explain the program, so I will reuse them here.

Capturing the concepts contained in Tic-Tac-Toe

Player

type Player = Cross | Circle;
  interface Circle { __type: "O";     }
  interface Cross  { __type: "X";     }

We use interface instead of type to get the type-level information (when you hover / or read a compile time error) to show Circle instead {__type: "Circle"} which it would do with type. It makes it a bit more pretty (not much more difference than that).

Square

type Square = Player | Empty;
  interface Empty  { __type: "Empty"; }

Size

// ##############################################
type Size = GameSize;
// ##############################################

The GameSize is set to 3 for this walk-through.
(Size was here before i made the UI at the top therefore the redeclaration)

Column & Row

// Column and Row can potentially be different sizes
// Note: winning on the diagonal will have to change
// If the game is not square.
type Column      = ToUnion<FromToInc<1,Size>>;
type Row         = ToUnion<FromToInc<1,Size>>;
type Coordinates = CartesianProductString<Column, Row>

The type of Column and Row is (in this case) 1 | 2 | 3. First, we generate numbers between 1 and Size which gives us[1,2,3] then we turn that into a union and end up with 1 | 2 | 3.

Coordiantes have the type instance of "22" | "21" | "23" | "12" | "11" | "13" | "32" | "31" | "33".

Utils used

// MinusOne<N>
// Defined between 1 and 1000
// Take a number N
// Check if length of empty array + 1 unknown element
// is equal to N, if it is, return length of array
// which then is one less then N.
// If not, recursively call MinusOne with an array
// that is one element longer.
type MinusOne<N extends number, Arr extends any[] = []> = [
  ...Arr,
  unknown
]['length'] extends N
  ? Arr['length']
  : MinusOne<N, [...Arr, unknown]>

// PlusOne<N>
// Defined between 0 and 999
// Start with an array of length 0 and check if it is
// equal to N.
// If it is add one element to the array and return
// it's length.
// If not recursively call PlusOne with an array that is
// one element longer.
// This way we get N + 1
type PlusOne<N extends number, Arr extends any[] = []> =
  [...Arr]['length'] extends N
    ? [...Arr, unknown]['length']
    : PlusOne<N, [...Arr, unknown]>

// FromToInc<Lower,Higher>
// Gives back an Array of all numbers
// between Lower and Higher (inclusive)
// Example: FromToInc<1,3> = [1,2,3]
type FromToInc<From extends number,
               To extends number,
               acc extends any[] = []> =
        From extends PlusOne<To>
          ? acc
          : FromToInc<PlusOne<From>, To, [...acc, From]>;

// FromToDec<Higher,Lower>
// Gives back an Array of all numbers
// between Higher and Lower (inclusive)
// Example: FromToDec<3,1> = [3,2,1]
type FromToDec<From extends number,
              To extends number,
              acc extends any[] = []> =
        From extends MinusOne<To>
          ? acc
          : FromToDec<MinusOne<From>, To, [...acc, From]>;

// Example: ToUnion<[1,2,3]> = 1 | 2 | 3
type ToUnion<T extends Array<any>> = T[number]

// something like
type Array<T> = { [index: number]: T ...}

// CartesianProduct<X,Y>
// Example:
// CartesianProduct<"a" | "b", "c" | "d"> = "ac" | "ad" | "bc" | "bd"
type CartesianProductString<T1 extends ToStringableTypes,T2 extends ToStringableTypes > = `${T1}${T2}`;
type ToStringableTypes = string | number | boolean | bigint;

type Cartesian...<T1 extends ... ,T2 extends ...> = ${T1}${T2}

T1 = "a" | "b" | "c"
T2 = "d" | "e" | "f"

${ "a" | "b" | "c" }${ "d" | "e" | "f" }

`a${"d"| "e" | "f"}` | `b${"d" | "e" | "f"}` | `c{"d" | "e" | "f"}`

"ad"| "ae" | "af" | "bd" | "be" | "bf" | "cd" | "ce" | "cf"

// Algebraic refactoring
 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 = 9
 "ad"| "ae" | "af" | "bd" | "be" | "bf" | "cd" | "ce" | "cf"

 (1 * (1 + 1 + 1)) + (1 * (1 + 1 + 1)) + (1 * (1 + 1 + 1)) = 9
 `a${"d"| "e" | "f"} | `b${"d" | "e" | "f"}` | `c${"d" | "e" | "f"}`

 (1 + 1 + 1) * (1 + 1 + 1) = 9
`${ "a" | "b" | "c" }${ "d" | "e" | "f" }`
 (3) * (3) = 9

// simplified
type AllCoordinates =
  CartesianProduct<Columns,Rows> = Col1Row1 | Col2Row1 | ... | Col1Row2

Side note

Actually, the type of Column and Row is 2 | 1 | 3. When you define a union like type A = 1 | 2 the type will become A = 2 | 1 which on the typelevel is equivalent, however, in this application, we very much care about traversal order and numbers being in order so we need to do some extra tricks sometimes to combat this. Maybe TypeScript makes no guarantees on the order of union members, so by scrambling them on purpose it hinders people from depending on something that is not part of the spec.

Winning positions

The way we are going to see if a player has won yet is by using the fact that we know what combination of positions are winning, if a player has all of them they have won. Steps:

1. Create a union of all the winning positions

   ["11", "12", "13"] | ["21", "22", "23"] | ...

2. Check what the current state of all of them are

   [Circle, Cross, Empty] | [Circle, Circle, Circle] ...

3. Create an intersection those states, and remove the array/tuple

   [Circle & Cross & Empty] | [Circle & Circle & Circle] | ...
   [never] | [Circle]
   never | Circle
   Circle

Only time we get a value is when all three are the same

Now we can check if the player is the winner, by checking if the intersection contains a player.

PlayerCircle extends Intersection ? true : false

// WinningPositions
// All the winning positions for a Tic-Tac-Toe game.
// Example
// ["11", "12", "13"] | ["21", "22", "23"] | ...
type WinningPositions =
  // Rows
  | GetRowPositions<Column, Row>
  // Columns
  | GetColumnPositions<Column, Row>
  // Diagonals
  | GetDiagonalPositions<Size>

// ###################################
// #### Winning Positions Helpers ####
// ###################################

type GetRowPositions<C extends Column, R extends Row> =
    R extends Row
      ? [CartesianProductString<C, R>]
      : never;

type GetColumnPositions<C extends Column, R extends Row> =
    C extends Column
      ? [CartesianProductString<C, R>]
      : never;

type GetDiagonalPositions<S extends Size> =
    StringConcatTuples<Diagonals<S>>

// Only first type parameter is allowed to be supplied
type Diagonals<
      Size extends number,
      _FromToSize extends number[] = FromToInc<1,Size>,
      _SizeToFrom extends number[] = FromToDec<Size, 1>,
      > =
    | Zip<_FromToSize, _FromToSize>
    | Zip<_FromToSize, _SizeToFrom>

WinningPositions is just the union of all positions that are winning. A position for us is just a combination(array) of coordinates. (A chess position is not just a bunch of squares but also the pieces on those squares so maybe WinningPositions is not the best name).

GetRowPositions and GetColumnPositions “iterates” through either row or column and then creates the Cartesian product between those values. In code, it would read something like

forEach(Row).map((r) => getCatesianProduct(Column, r))

So the output is ["11", "21", "31"] | ["21", "22", "23"] ... for Row for example. When you do R extends Row ? ... | ... in TypeScript, that is “looping” over R and creating a union of all the results. The details of this are discussed in great detail in the UnionToIntersection util explanation.

Diagonals have two parameters that are not allowed to be used when calling the type-level function. This is so they can be used to bind the result of a typelevel function to allow for reuse in the function body.

Here we are generating two arrays [1,2,3] and [3,2,1] and then we do two Zip operations

Zip<[1,2,3],[1,2,3]>

and

Zip<[1,2,3],[3,2,1]>

which produces [[1,1],[2,2],[3,3]] and [[1,3],[2,2],[3,1]]

We then turn each tuple into strings using StringConcatTuples in GetDiagonalPositions. Resulting in ["11", "22", "33"] and ["13", "22", "31"].

Utils used

// Zip two arrays together
// Example:
// Zip<[1,2,3],["a","b","c"]> = [[1,"a"],[2,"b"],[3,"c"]]
type Zip<
      T extends any[],
      U extends any[],
      Acc extends any[] = []
      > =
  T extends [infer Head, ...infer Tail] ?
  U extends [infer Head2, ...infer Tail2] ?
  Zip<Tail, Tail2, [...Acc, [Head, Head2]]> : Acc  : Acc;

// Join tuples together to strings
// Example:
// StringConcatTuples<[[1,2],[3,4]]> = ["12","34"]
type StringConcatTuples<T extends [number, number][]> =
  {[Key in keyof T]: `${T[Key][0]}${T[Key][1]}`};

Board

// Fundamental data type of the game.
// Board contains a mapping from Coordinate to Square
// A Square is either Empty, Cross, or Circle.
type Board = { [s in Coordinates]: Square };

Game States

// The game can be in one of three states:
// 1. Round in progress
// 2. Won
// 3. Draw
type GameStates =
  | Round<any, any, any>
  | Winner<any, any, any>
  | Draw<any, any>

Round

// ###################################
// ####           Round           ####
// ###################################
//
// A Round has a bunch of Squares and a Player that is next
// to move. It also has a previous Round or Nil,
// to be able to allow for undoing moves.
interface Round<
  B extends Board,
  P extends Player,
  R extends Round<any, any, any> | Nil
> extends HasPrevious<R> {
  __tag: "round";
  board: B;
  nextToMove: P;
}
  interface Nil    { __type: "Nil";   }

// We separate our HasPrevious interface from the
// Round interface.To be able to use it in other interfaces.
// And have type level functions where the only
// constraint is that it has the HasPrevious interface.
interface HasPrevious<R> {
  previous: R;

Winner

interface Winner<
  S extends Player,
  PrevR extends Round<any, any, any>,
  Curr extends Board
> extends HasPrevious<PrevR> {
  __tag: "winner",
  winningPosition: Curr;
  winner: S;
}

Draw

interface Draw<R extends Round<any, any, any>>
    extends HasPrevious<R> {__tag: "draw";}

Initial board & round

type InitialBoard = { [key in keyof Board]: Empty };
type InitialRound = Round<InitialBoard, Cross, Nil>;

Game State Helpers

type GetBoard<R extends GameStates>
                  =
                    R extends Draw<any, infer B>         ? B
                  : R extends Round<infer B, any, any>   ? B
                  : R extends Winner<any, any, infer B>  ? B
                  : never;

Game actions

Move

There is only one action, it’s to make a move.

// ...
// Last two arguments are not allowed to be passed in,
// It's used to reduce duplication in the function body.
type Move<
  CurrentRound extends Round<Board, P, any>,
  P extends Player,
  Position extends AvailableSquares<CurrentRound["board"]>,
  _NextBoard extends Board =
    SetSquare<CurrentRound["board"], Position, P>,
  _NextRound extends Round<any,any,any> =
    Round<_NextBoard, GetNextPlayer<P>, CurrentRound>
> =
HasWon<P,_NextRound> extends true ?
  ? Winner<P, CurrentRound, _NextBoard>
  : NoMoreSquares<_NextBoard> extends true
    ? Draw<CurrentRound, _NextBoard>
    : _NextRound

Move steps:

1. Check if the position is part of AvailableSquares[CurrentRound['board']]
2. Create two variables, which are the board and round after the move has been applied _NextBoard and _NextRound
3. Check if player has won in the _NextRound, if true return Winner<P, ...>
4. Check if the game will have no more squares after this move, if true return Draw<...>
5. Else return next Round.

Game state functions

Available Squares

// Squares that are possible to play on
type AvailableSquares<B extends Board> = {
  [Coordinate in keyof B]: B[Coordinate] extends Empty ?
        Coordinate
      : never;
}[keyof B];

AvailableSquares loops through the coordinates and replaces every square with either the Coordinate or never

{
 "11": never,
 "12": "12",
 ...
}

We then lookup all values for all keys with [keyof B] this produces a union like never | "12" | ... and since never represents the absence of a value. never gets removed from unions leaving only the squares that are possible to play.

Get next player

Toggles between the players

type GetNextPlayer<P extends Player> =
  P extends Cross ? Circle : Cross;

Set square

Find and replace what is on a square, by looping through all coordinates until we find the one we want to set.

// Sets a Square to a Player
type SetSquare<B extends Board, CoordinateToSet, Player> = {
  [Coord in keyof B]: Coord extends CoordinateToSet ?
      Player
    : B[Coord];
};

No more squares

If the Board extends never that means there was nothing in the union returned by AvailableSquares<B>, thus there are no more squares to play on.

type NoMoreSquares<B extends Board> =
  AvailableSquares<B> extends never ? true : false;

Get winner

// If there is a winner in the Squares provided then
// the winner is returned.
type GetWinner<B extends Board> =
   UniqueInSequence<LookupCoordinates<WinningPositions,B>>

// LookupPosition returns the state of the squares
// at each position listed
// ["11", "12", "13"] | ... -> [Circle, Circle, Circle] | ..
type LookupCoordinates<
        Coords extends Array<Coordinates>,
        B extends Board> =
    { [Key in keyof Coords ]: B[Coords[Key]] }

// If there is any Array that contains only the same element
// then that element will be returned
type UniqueInSequence<P extends Array<unknown>> =
  P extends Array<unknown> ?
    UnionToIntersection<P[number]> : never

We use the WinningPositions together with a Board to look up the state of all those winning tuples. We then see if any of those tuples of coordinates only contain one player.

GetWinner might not be the perfect name, because it gives back whatever is unique in a winning set of squares so for example it would return Empty for the initial board. (So the game starts out with Empty as a winner one could say)

Utils used

// UnionToIntersection<X>
// Takes a union like `A | B | C` and
// returns an intersection like `A & B & C`
type UnionToIntersection<U> =
  _PutUnionMembersIntoFunctionArgumentPosition<U> extends
      ((k: infer I)=>void)
          ?  I
          : never

type _PutUnionMembersIntoFunctionArgumentPosition<U> =
      U extends any
        ? (k: U)=>void
        : never;

type _PutUnionMembersIntoFunctionArgumentPosition<U> =
      U extends any
        ? (k: U)=>void
        : never;

type _PutUnionMembersIntoFunctionArgumentPosition<U> =
      U extends any
        ? (k: U)=>void
        : never;

type ABC = "a" | "b" | "c"
type _ = _PutUnionMembersIntoFunctionArgumentPosition<ABC>

  "a" extends any ? (k: "a")  => void : never
| "b" extends any ? (k: "b")  => void : never
| "c" extends any ? (k: "c")  => void : never

  (k: "a")  => void
| (k: "b")  => void
| (k: "c")  => void

_PutUnionMembersIntoFunctionArgumentPosition<"a"|"b"|"c">
("a" | "b" | "c") extends any ?
  (k: "a" | "b" | "c")  => void : never

_PutInFunctionArgumentPosition<U> =
    [U] extends [any]
        ? (k: U)=>void
        : never

type ABC = "a" | "b" | "c"
type _   = _PutInFunctionArgumentPosition<ABC>

(["a" | "b" | "c"] extends [any] ?
    (k: "a" | "b" | "c")=>void : never)

(k: "a" | "b" | "c") => void

type ABC  = "a" | "b" | "c"
type ABC3 = ABC | 3

type ABC_Inline_Extends_A      = ABC extends   "a"    ?
                                     (k: ABC) => void
                                    : never
type Naked_Extends_A<T>        =  T  extends   "a"    ?
                                     (k:  T ) => void
                                    : never
type Naked_Extends_String<T>   =  T  extends  string  ?
                                     (k:  T ) => void
                                    : never
type Clothed_Extends_String<T> = [T] extends [string] ?
                                     (k:  T ) => void
                                    : never

...PART1 extends ((k: infer I)=>void) ? I : never

  (k: "a")  => void
| (k: "b")  => void
| (k: "c")  => void

(    (k: "a")  => void)
   | (k: "b")  => void)
   | (k: "c")  => void)
) extends ((k: infer I)=>void) ? I : never

((k: infer I) => void)

     (k: "a") => void
  or (k: "b") => void
  or (k: "c") => void

((k: infer I) => void)

type T = (k: HasName) => void | (k: HasAge) => void
const func : T = ...

   (k: HasName) => void
or (k: HasAge)  => void

type Dog = HasName & HasAge
const dog : Dog = createDog("Fido", 3)
func(dog)

Has Won

type HasWon<
  P extends Player,
  B extends Round<any, any, any>
> = P extends GetWinner<B["squares"]> ? true : false;

Extra functions from requirements

Who won or draw ?

Just a function that gives back a string informing who won or if it’s a draw, only possible to call when the game state is either Draw or Winner

type WhoWonOrDraw<
    A extends Draw<any,any>
  | Winner<Player, any, any>> = (
  state: A
) => A extends Winner<infer P, any, any>
  ? PlayerWinnerString<P>
  : DrawString;
  type DrawString = "The game was a draw";

type PlayerWinnerString<P extends Player> =
  P extends Circle ?
    CircleWonString
  : CrossWonString
  type CircleWonString = "Circle Won the game"
  type CrossWonString = "Cross Won the game"

Take move back

Any round except the initial round has a previous round. This function gives back that previous round.

type TakeMoveBack<
        R extends HasPrevious<Round<any, any, any>>
        > =
        R["previous"];

Is position occupied?

type IsPositionOccupied<
  RW extends Winner<any, any, any> | Round<any, any, any>,
  Coord extends Coordinates,
  B extends Board = GetBoard<RW>
> = (
  B[Coord]
) extends Empty
  ? false
  : true;

That is all the code related to the fundamentals of the game!

There is some extra code for the ‘Game UI’ to play the game in a nicer way than you will see in the tests. We will go through that code last.

Tests

Note, since these are typelevel tests we want to be able to test that we do get type-errors, when we should while allowing the program to compile. TypeScript gives us this handy comment we can use to check for type errors.

@ts-expect-error

@ts-expect-error gives an error if there is no error.

I have hidden the tests in a collapsible section, so you can skip them if you want.

Test Utils

To be able to write any useful tests we need equality! How do you check if two types are Equal?

Once again type-challenges to the rescue!

The Equal and Expect functions used in the tests have been taken directly from type-challenges repo.

Equal

Equal<X,Y>
Check if two types are equal.

type Equal<X, Y> =
  (<T>() => T extends X ? 1 : 2) extends
  (<T>() => T extends Y ? 1 : 2) ? true : false;

For full discussion around this function see this TypeScript issue

…It relies on conditional types being deferred when T is not known. Assignability of deferred conditional types relies on an internal isTypeIdenticalTo check, which is only true for two conditional types if:

• Both conditional types have the same constraint
• The true and false branches of both conditions are the same type

- fatcerberus

Expect

// Expect<T>
// Give type-level error if T is not true
type Expect<T extends true> = T;

// ##################################
// #              TEST              #
// ##################################
// #         Correct strings        #
// ##################################
type CircleWonStringTest =
  Expect<
      Equal<
          ReturnType<WhoWonOrDraw<WinCircleFinal>>,
          CircleWonString
          >
        >;

type CrossWonStringTest =
  Expect<
      Equal<
          ReturnType<WhoWonOrDraw<WinCrossFinal>>,
          CrossWonString
          >
        >;

type DrawStringTest =
  Expect<
      Equal<
          ReturnType<WhoWonOrDraw<DrawFinal>>,
          DrawString
          >
        >;

// ##################################
// #              TEST              #
// ##################################
// #         No double moves        #
// ##################################
// @ts-expect-error
type NoDoubleMove = Move<
                      Move<InitialRound, Cross, "33">,
                                         Cross, "13">;

// ##################################
// #              TEST              #
// ##################################
// #      No start with Circle      #
// ##################################
// @ts-expect-error
type NoStartWithCircle = Move<InitialRound, Circle, "33">;


// ##################################
// #              TEST              #
// ##################################
// #      No taking a used square   #
// ##################################
// @ts-expect-error
type NoTakingAUsedSquare =
  Move<
    Move<
      InitialRound, Cross,  "33">,
                    Circle, "33">

// ##################################
// #              TEST              #
// ##################################
// #  InitialRound has no previous  #
// #  Don't allow to take too many  #
// #           moves back           #
// ##################################
// @ts-expect-error
type NotToManyMovesBack = TakeMoveBack<InitialRound>;


// ##################################
// #              TEST              #
// ##################################
// #         Making a move          #
// #       and taking it back       #
// #   Gives back the start state   #
// ##################################
type MoveOne      = Move<InitialRound, Cross, "33">;
type BackToNormal = TakeMoveBack<MoveOne>;
type Outcome      = Expect<
  Equal<
    InitialRound,
    BackToNormal
  >>;

type BackFromDraw = Expect<
                      Equal<
                        TakeMoveBack<DrawFinal>,
                        DrawStep8
                           >
                          >;
type BackFromWin = Expect<
                      Equal<
                        TakeMoveBack<WinCrossFinal>,
                        WinCrossStep4
                            >
                          >;

// ##################################
// #              TEST              #
// ##################################
// #       IsPositionOccupied       #
// ##################################
type Test = Expect<
  Equal<IsPositionOccupied<WinCrossFinal, "12">, false>
>;

type Test2 = Expect<
  Equal<
    IsPositionOccupied<WinCrossFinal, "33">,
    true
  >>;

type Test3 = Expect<
  Equal<
    IsPositionOccupied<InitialRound, "33">,
    false
  >>;

// @ts-expect-error
type Test4 = Expect<
  Equal<
    IsPositionOccupied<InitialRound, "33">,
    true
  >>;

// ##################################
// #              TEST              #
// ##################################
// #    GAME That ends in a draw    #
// ##################################
type DrawStep1 = Move<InitialRound, Cross, "13">;
type DrawStep2 = Move<DrawStep1, Circle, "23">;
type DrawStep3 = Move<DrawStep2, Cross, "33">;
type DrawStep4 = Move<DrawStep3, Circle, "12">;
type DrawStep5 = Move<DrawStep4, Cross, "22">;
type DrawStep6 = Move<DrawStep5, Circle, "11">;
type DrawStep7 = Move<DrawStep6, Cross, "32">;
type DrawStep8 = Move<DrawStep7, Circle, "31">;
type DrawFinal = Move<DrawStep8, Cross, "21">;
type DrawOutcome = Expect<
  Draw<any> extends DrawFinal ? true : false
  >;


// ##################################
// #              TEST              #
// ##################################
// #     GAME That Cross Wins       #
// ##################################
type WinCrossStep1 = Move<InitialRound, Cross, "13">;
type WinCrossStep2 = Move<WinCrossStep1, Circle, "11">;
type WinCrossStep3 = Move<WinCrossStep2, Cross, "33">;
type WinCrossStep4 = Move<WinCrossStep3, Circle, "21">;
type WinCrossFinal = Move<WinCrossStep4, Cross, "23">;
type WinCrossOutcome = Expect<Equal<
   WinCrossFinal["winner"], Cross
>>;

// ##################################
// #              TEST              #
// ##################################
// #     GAME That Circle Wins      #
// ##################################
type WinCircleStep1 = Move<InitialRound, Cross, "13">;
type WinCircleStep2 = Move<WinCircleStep1, Circle, "11">;
type WinCircleStep3 = Move<WinCircleStep2, Cross, "33">;
type WinCircleStep4 = Move<WinCircleStep3, Circle, "21">;
type WinCircleStep5 = Move<WinCircleStep4, Cross, "22">;
type WinCircleFinal = Move<WinCircleStep5, Circle, "31">;
type WinCircleOutcome = Expect<Equal<
   WinCircleFinal["winner"], Circle
>>;

UI

I know it’s a bit silly to call this a UI, but hey, it gives you visual indications of the state of the game and yells at what you are doing wrong if you try to play the game incorrectly. So that is a rudimentary UI.

Display

Current state highlighting

Error handling

// To play along
// Copy the code into the TypeScript playground
// https://www.typescriptlang.org/play
//
//
// ##################################
// ##################################
// #          Play a Game           #
// #              of                #
// #--------------------------------#
// #           Typelevel            #
// #          Tic-Tac-Toe           #
// #--------------------------------#
// #              UI                #
// #          STARTS HERE           #
// ##################################
// ##################################
//
// This is my attempt of a decent UX (hehe).
// 0. Select game board size (3 => 3x3, 4 => 4x4, etc)
// 1. Cross will be the first to move
// 2. Just enter coordinates as number
//    (13 => Coordinate(x=1, y=3))
//
// The status checks below will turn RED
// To show what state the game is in.
//
// Illegal moves will be compile-time errors
// with decent error messages.
//
// Hover ___DISPLAY__ for a visual representation
// of the current state of the game.
type GameSize = 3;

//   ##############################
type ____________DISPLAY___________ = d
//   ##############################

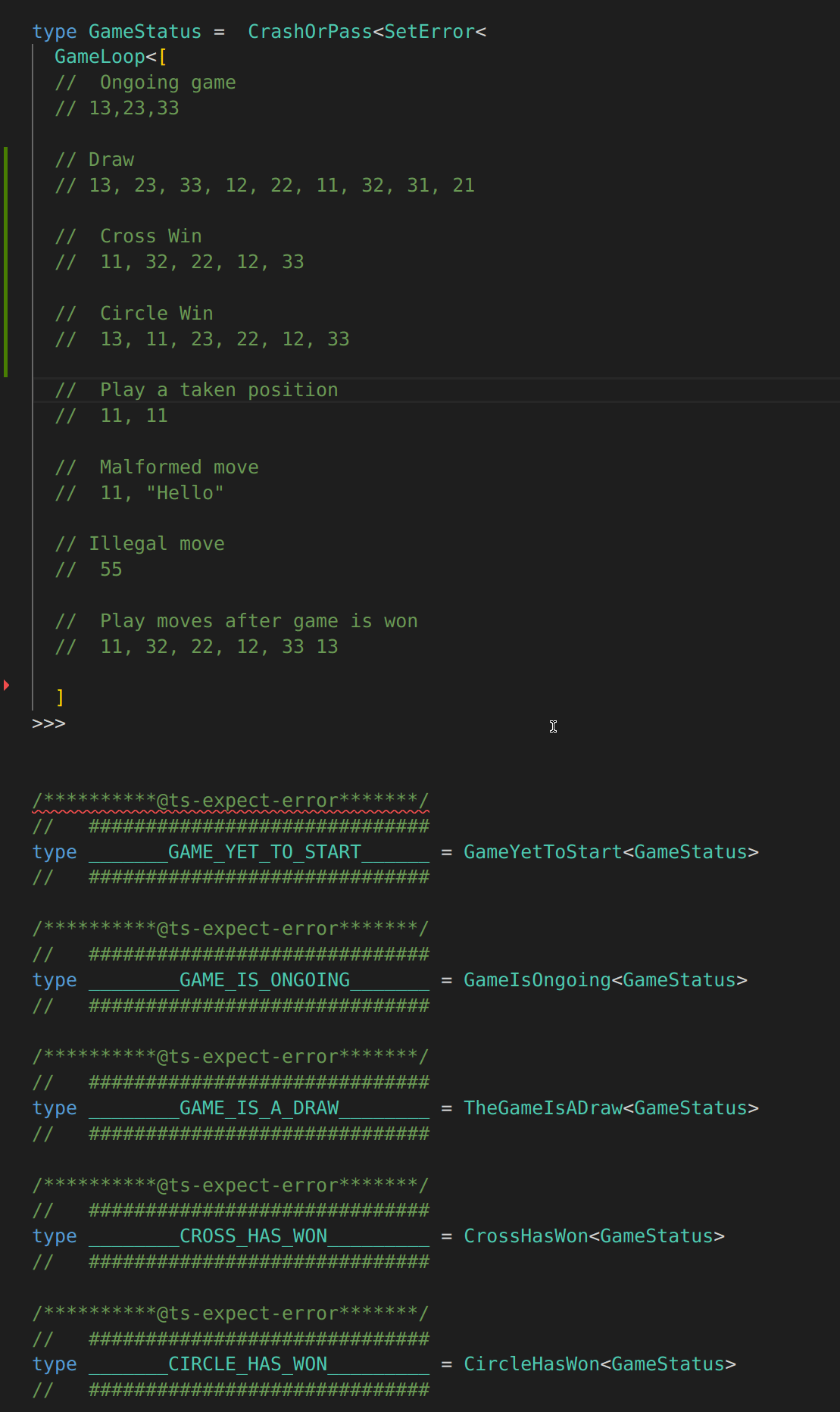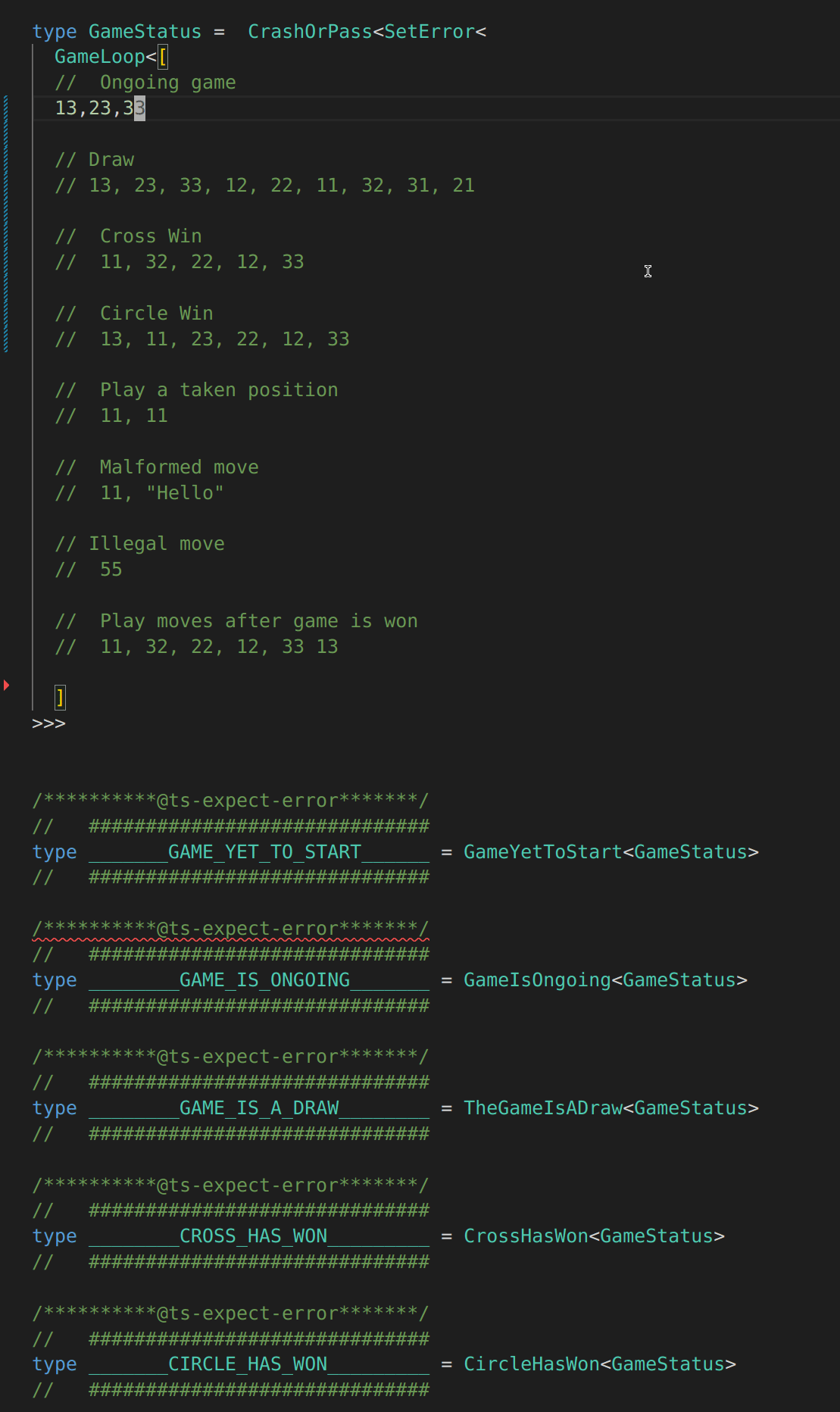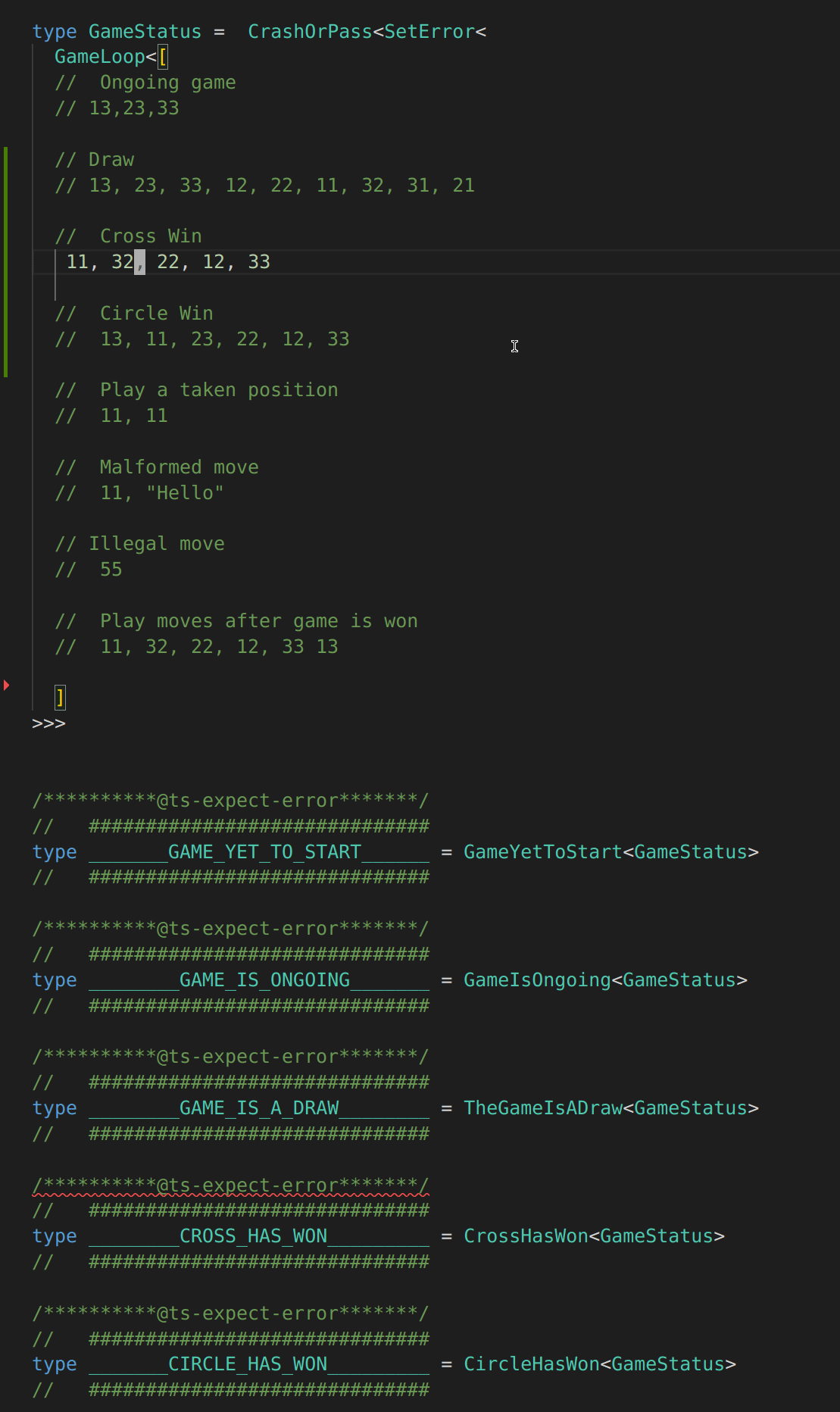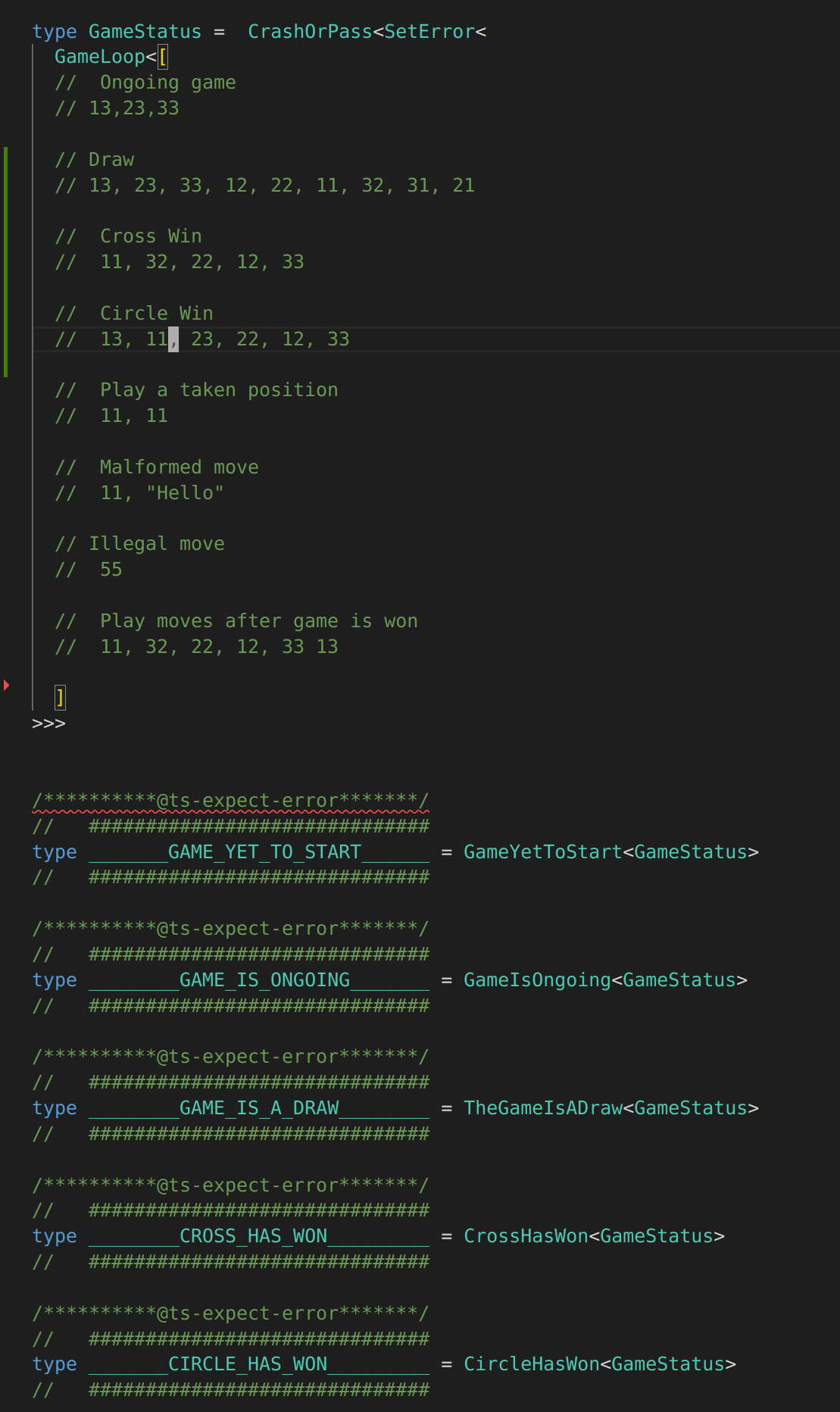
type GameStatus =  CrashOrPass<SetError<
  GameLoop<[
  //  Ongoing game
  // 13,23,33

  // Draw
  // 13, 23, 33, 12, 22, 11, 32, 31, 21

  //  Cross Win
  //  11, 32, 22, 12, 33

  //  Circle Win
  //  13, 11, 23, 22, 12, 33

  //  Play a taken position
  //  11, 11

  //  Malformed move
  //  11, "Hello"

  // Illegal move
  //  55

  //  Play moves after game is won
  //  11, 32, 22, 12, 33 13

  ]
>>>


/**********@ts-expect-error*******/
//   ##############################
type _______GAME_YET_TO_START______ =
        GameYetToStart<GameStatus>
//   ##############################

/**********@ts-expect-error*******/
//   ##############################
type ________GAME_IS_ONGOING_______ =
        GameIsOngoing<GameStatus>
//   ##############################

/**********@ts-expect-error*******/
//   ##############################
type ________GAME_IS_A_DRAW________ =
        TheGameIsADraw<GameStatus>
//   ##############################

/**********@ts-expect-error*******/
//   ##############################
type ________CROSS_HAS_WON_________ =
         CrossHasWon<GameStatus>
//   ##############################

/**********@ts-expect-error*******/
//   ##############################
type _______CIRCLE_HAS_WON_________ =
        CircleHasWon<GameStatus>
//   ##############################

// ##################################
// ##################################
// #--------------------------------#
// #           Typelevel            #
// #          Tic-Tac-Toe           #
// #--------------------------------#
// #              UI                #
// #           ENDS HERE            #
// #--------------------------------#
// ##################################
// ##################################

Ui Code

UI Helpers

// 'd' is just to hide the variable as
// much as possible in the UI above
type d = ShowBoard<GetBoard<GameStatus>>

// These are functions give type errors when the game is
// not in their state.Then we combine that with
// @ts-expect-error to flip that behavior
type TheGameIsADraw<T extends Draw<any, any>> = T
type CrossHasWon   <T extends Winner<Cross, any, any>>= T
type CircleHasWon  <T extends Winner<Circle, any, any>> = T
type GameIsOngoing <T extends
                    Round<any, any, Round<any,any,any>>> = T
type GameYetToStart<T extends InitialRound> = T

I use @ts-expect-error to turn the type errors around. So it shows an error when the types actually type check. That is useful here, in the absence of something like “extends everything except X”.

type CrossHasWon<T extends Not<Winner<Cross,any,any>>> = T

Game Loop

type GameLoop<A extends Array<number>,
              R extends Round<any,any,any> = InitialRound,
              P extends Player = Cross> =
  A extends [infer Head, ...infer Tail] ?
    Head extends number ?
      Tail extends Array<number> ?
        NumToStr<Head> extends Coordinates ?
          NumToStr<Head> extends AvailableSquares<R["board"]> ?
            Move<R,P,NumToStr<Head> > extends Round<any,any,any> ?
              GameLoop<Tail, Move<R,P,NumToStr<Head> >, GetNextPlayer<P>> :
              Tail extends [] ?
                Move<R,P,NumToStr<Head> >
                : GAME_ERROR<`No more moves allowed, game is over`>
          : GAME_ERROR<`Square '${Head}' already taken`>
        : GAME_ERROR<`Coordinate '${Head}' is illegal`>
      : GAME_ERROR<`Tail of Coordinate array is malformatted`>
    : GAME_ERROR<`Coordinate '${Head extends ToStringableTypes ? Head : never}' is not a number`>
  : R

type GAME_ERROR<T extends string> = `__ERROR__: ${T}`
type SetError<T> = [T, T extends GAME_ERROR<string> ? "error" : "noError"]
type CrashOrPass<T extends [unknown, "noError"]> = T[0];
type NumToStr<N extends number> = `${N}`

First of we create some data abstraction in that we allow the players to enter number instead of Coordinate then we do some conditional checks to see if that number can be cast into a Coordinate this makes the UI easier to use since we don’t have to add "" around all moves.

We are kind of able to simulate X extends not<...> (i.e type-error if X does extend) a bit with SetError and CrashOrPass which needs to be used together, I don’t know how to put them together into one typelevel function or even better get GameLoop to have this constraint by itself. With more work, it’s probably possible.

GameLoop is a recursive typelevel function that ends when the game ends or an error occurs. The errors give informative information like __ERROR__: Square '${Head}' already taken I think it’s really cool that we can just inject Head into a string and get type errors like

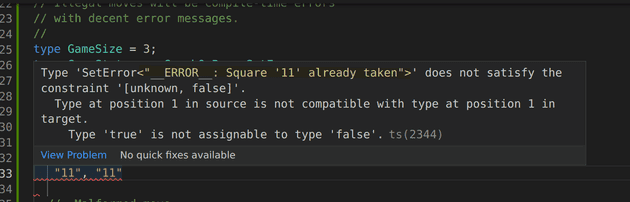
To not just get a return type of a custom error but actually get a compile-time error highlighting it we wrap GameLoop in SetError and CrashOrPass.

type SetError<T> = [T,
                    T extends GAME_ERROR<string> ?
                        "error"
                      : "noError"
                   ]

If the return type that extends GAME_ERROR<string> then set the second value in the tuple to "error".

CrashOrPass then takes the return type from SetError and if the second value is not "noError" we get a compile time error, which is exactly what we want.

type CrashOrPass<T extends [unknown, "noError"]> = T[0];

If we do not get a compile-time error the first value of the tuple is returned which is just non-error type.

(In TypeScript types propagate if possible even if there is a type-error, like here T[0] is not the part with the type-error so that propagates. We use this to also show the error in ___DISPLAY___)

I know it’s common in Erlang and Elixir to follow this type of pattern on the value level. by returning {:ok, data } | {:error, reason}.

Display

Best for last, the display is the coolest feature! We want to produce a UI like

{
  [X,X,O],
  [X,_,O],
  [_,_,O],
}

To show the state of the game when hovering the type

We use the Board, to first change the Squares from Circle | Cross | Empty to X | O | _

Then it’s a matter of producing a layout that the type-checker will display in a nice way. String was no good because multiline strings become XXO\nX_O\n__O. Multidimensional arrays are also just one line [[X,X,O],[X,_,O],[_,_,O]]` So settled for an object where the keys are the rows.

{
  3: [X,X,O],
  2: [X,_,O],
  1: [_,_,O],
}

// Show the state of the game when hovering the type instantiated type
type PrintGameDisplay<T extends (GameStates | GAME_ERROR<string>)> =
  T extends GameStates ? ShowBoard<GetBoard<T>> : T

// Some shorter and nicer looking symbols for the Display
interface X {}
interface O {}
interface _ {}

// UIBoard
// Coordinates to something that we want to Display
type UIBoard = {[s in Coordinates]: unknown}

/// #### DISPLAY HELPERS ####

type ShowBoard<B extends Board> = ShowUIBoard<ToUIBoard<B>>;

// ToUIBoard
// The particular board we want to show
// Structurally, a UIBoard
type ToUIBoard<B extends Board> =
  {[s in Coordinates]: ChangeSquare<B[s]>};

type ChangeSquare<S extends Square> = S extends Cross  ? X
                                    : S extends Circle ? O
                                    : S extends Empty  ? _
                                    : never;

// We want our coordinate system to have 1,1 bottom left
// and Size,Size top right
type RowsBackwards  = FromToDec<Size,1>
type ColumnsForward = FromToInc<1,Size>

// ShowUIBoard
type ShowUIBoard<B extends UIBoard > =
  {[key in keyof RowsBackwards as KeyToValue<RowsBackwards,key>]: RowsBackwards[key] extends number
    ? TupleCoordinateLookups<Zip<ColumnsForward,Repeat<RowsBackwards[key], Size>>, B> : never}

  type KeyToValue<T extends Array<unknown>, K extends keyof T> =
      K extends `${number}` ? T[K] : never;

  type Repeat<T, N extends number, arr extends Array<T> = []> =
      N extends 0 ? arr : Repeat<T, MinusOne<N>, [T, ...arr]>;

  type TupleCoordinateLookups<T extends [number, number][], B extends UIBoard> =
    {[Key in keyof T]: TupleCoordinateLookup<T[Key], B>};

  type TupleCoordinateLookup<T extends [number, number], B extends UIBoard> =
    `${T[0]}${T[1]}` extends keyof B ? B[`${T[0]}${T[1]}`] : never;
// ShowUIBoard End

I indented the types that are just helpers for ShowUIBoard. We only have some limited ability to create named type variables in a scope which I have already shown, <..., MyType = MyTypeFunc<T>> So here is another approach based only on convention and there to make the code easier to browse. When you have access to creating multiple files you can ofc create your scope that way.

ToUiBoard loops through all Coordinates and maps the members of the Square type to another type that we would like to display.

ShowUIBoard uses one trick we have not seen yet. https://www.typescriptlang.org/docs/handbook/2/mapped-types.html#key-remapping-via-as it’s the as syntax that lets us change the key while we are mapping. That is perfect here because we use the keys 0,1,2, ...Size in RowsBackwards to be mapped to the value at each index, so we get the rows of our display object.

ex. RowArray[0] value is Size RowArray[0] value is Size-1

{
  [Size]    : ...,
  [Size - 1]: ...,
  [Size - 2]: ...,
}

Then for the values on each row we combine the column values together with the current row value, by using the Zip operation, where the second argument is just the row repeated column length times.

Zip([1,2,3], [3,3,3]) = [[1,3],[2,3],[3,3]]

Then we do a lookup for each tuple [x,y] to get the corresponding symbol representing the state. We do that by first turning [x,y] into a string ${x}{y} and the end result is an object that looks like this.

{
  3: [X,X,O],
  2: [X,_,O],
  1: [_,_,O],
}

And this is our display! Now we have everything we need to produce the final product.

Closing thoughts

Thanks for reading this far! I hope you learned something on this journey. TypeScript is very powerful and you can basically do anything you want as long as you are willing to spend enough time. It just gets more and more awkward to achieve the constraints on the typelevel. I would not say that this is any good practice in general, but knowing that something is possible could make it worth exploring in cases where it would be worth the end result.

A few years ago I was of the opinion that if you could have static guarantees you should. Now I still want those guarantees but I think it’s very prudent and acceptable to use something like type guards

if(isDog(x)){
  //do something
}

And write code that is still safe but does runtime checks, usually this lead to simpler solutions.

Don’t forget to check out The Advanced Software Design Course.

Cheers!